 Method 2: Trigonometry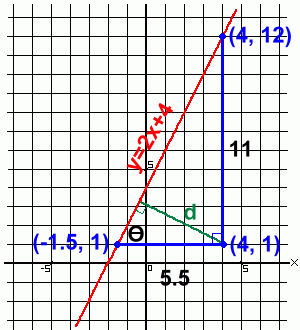 
Using this method, we will first construct a right triangle by drawing a horizontal and vertical line to y=2x+4 from the point (4, 1). Knowing the length of these sides, we'll then find angle Θ using the big triangle, and then use Θ to solve for d in the lower small triangle.Step 1: Draw the Lines Draw a horizontal line from (4, 1) to the line y=2x+4. It meets the line at a point with y coordinate 1. Substituting y=1 in the line equation y=2x+4 yields the value of -1.5 for x. So the left corner of the triangle is (-1.5, 1). Draw a vertical line from (4, 1) to the line y=2x+4. It meets the line at a point whose x coordinate must be 4. Substituting x=4 in the line equation y=2x+4 yields the value of 12 for y. So the top corner of the triangle is (4, 12). Step 2: Find Θ Given where angle Θ is, we now know that: - the opposite side of the large triangle has length 11 - the adjacent side has length 5.5.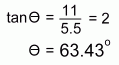 
Step 3: Find d: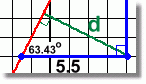 
Using the small triangle, we know an angle, and the hypotenuse 5.5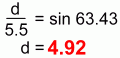
Method 2 gives an answer of 4.92 for the distance from point (4, 1) to line y=2x+4 |