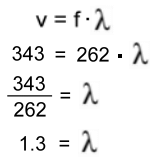 Music is the sound that is produced by instruments or voices. To play most musical instruments you have to create standing waves on a string or in the air in a tube or pipe. A standing wave pattern is when a wave oscillates but doesn't appear to move. This is actually caused by the superposition of two or more waves, travelling in different directions but each having the same frequency. Before we continue with the explanation about how tube instruments using air, like flutes or clarinets, produce sounds, have a look at our page about waves and wavelengths to become familiar with sound waves. 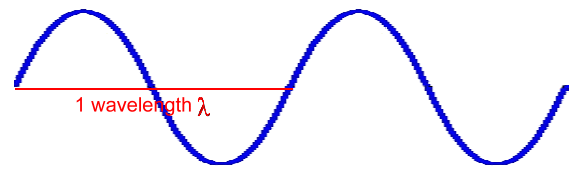 A sound wave's length is its wavelength, represented by the symbol 'lambda' λ. The frequency f of a wave is the number of full wavelengths that pass by in one second. It's measured in waves per second, or hertz. For example, middle C on a piano has a frequency of about 262 Hz (Hertz is waves per second), which means that 262 waves pass by every second. The wavelength of these waves is 1.3 metres. The relation between frequency and wavelength is dependent on the speed of sound, which is 343 m/s in air at room temperature. The relationship is: Speed = frequency x wavelength 
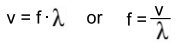 As one increases, the other decreases, and vice versa. Now we're ready to look at what happens to sound waves when they enter a tube. We're going to look at two different cases: a tube where both ends are open, like a flute, and a tube where one end is closed, like pan pipes (plugged at the bottom) or a clarinet (closed at your mouth).  
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude does not move in space. Standing waves are the result of interference between two waves traveling in opposite directions. The most common cause of standing waves is the phenomenon of resonance, in which standing waves occur inside a resonator due to interference between waves reflected back and forth at the resonator's resonant frequency. A standing wave, also called stationary wave, is a combination of two waves moving in opposite directions, each having the same amplitude and frequency. The phenomenon is the result of interference; when waves are superimposed, their energies are either added together (at the peaks, called antinodes) or canceled (at the red dots, called nodes).  The pitch of the sound is related to the frequency of the wave. The higher the frequency, the higher the pitch. Wind instruments produce sounds by means of vibrating air columns. To play a wind instrument you push the air in a tube with your mouth or a reed. The air in the tube starts to vibrate with the same frequency as your lips or the reed. Resonance increases the amplitude of the vibrations, which can form standing waves in the tube. The length of the air column determines the resonant frequencies. The shorter the tube the higher the pitch. Many instruments have holes, whose opening and closing controls the effective pitch. We can create a standing wave in a tube which is open on both ends, and in a tube which is open on one end and closed on the other end. Open and closed ends reflect waves differently. When looking at a standing wave, some points don’t move at all and others seem to be vibrating the most. The points that are still are called 'nodes'. Nodes are points along the tube of vibrating air where there is no movement - they are the points of destructive interference. At these points, the two interfering waves are out of phase, meaning the crests of one wave align with the troughs of the other, canceling each other out. The points with the maximum movement are 'antinodes'. Antinodes are points of constructive interference where the vibrating air has maximum displacement. Here, the interfering waves are in phase, meaning the crests of one wave align with the crests of the other, resulting in amplified wave amplitude. Sound at the desired pitch emanates from the tube's end or ends when there are antinodes there. Harmonics refers to the various patterns a standing wave can form in the tube. Harmonics are integral multiples of the fundamental frequency of a wave. When air is blown through a pipe, it can vibrate at several different frequencies simultaneously. Each of these frequencies corresponds to a different mode of vibration, or harmonic, and contributes to the overall sound produced. Tubes with two open ends The longest standing wave in a tube of length L with two open ends has antinodes (pressure nodes) at both ends. It is called the fundamental or first harmonic, and is one half a wavelength long: 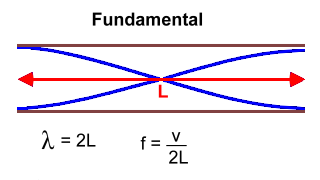 The next longest standing wave in a tube of length L with two open ends is the second harmonic. It also has antinodes at each end. It is two half-wavlengths long. 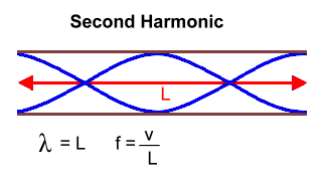 For a tube with two open ends, all frequencies fn = nf1, where n is an integer, are natural frequencies. In other words, all natural frequencies are a multiple of the fundamental frequency. Tubes with one open and one closed end The longest standing wave in a tube of length L with one open end and one closed end has an antinode at the open end and a node at the closed end. This is the fundamental, and is one quarter of a wavelength long. 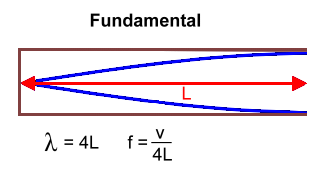 The next longest standing wave in a tube of length L with one open end and one closed end is the third harmonic. 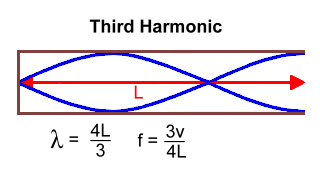 For a tube with one open and one closed end, all frequencies fn = nf1, where n is an odd integer are natural frequencies. In other wordss, the natural frequancies are odd multiples of the fundamental frequency. Sample Problems 1. What length should a pipe open at both ends be, to produce a fundamental frequency of 110 Hz on a day when the speed of sound is 343 m/s? Solution: One half wavelength has to fit into the tube of length L By rearranging the equation for f for a tube open at both ends: f = v/2L >>> L = v/2f = 343/2(110) = 1.55 m 2. Why does a flute play a higher note than a clarinet, when both are about the same length?  Solution: If they're both playing their lowest note The clarinet is closed at one end, where the lips are. The wavelength of the fundamental standing wave: λ = 4L A flute is a tube with two open ends. Wavelength of the fundamental standing wave: λ = 2L, which is shorter (L being the same for both). A shorter wavelength means a higher frequency. |
