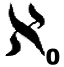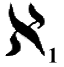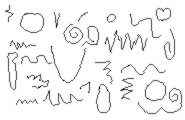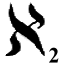You may be familiar with the concept of infinity, a number which cannot be written, one which is unimaginably large.
You may be familiar with the concept of infinity, a number which cannot be written, one which is unimaginably large.
The familiar symbol for infinity is the sideways 'eight':
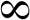
and is most familiar as 'where you will end up if you can ever count all of the Natural numbers':
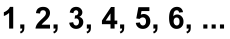
How many numbers are there? There are an infinite number of them. So far, so good. But there are some interesting properties of infinity that you may not have been aware of, and there is actually more than one infinity. Let's find out more ...
|
Infinity is a number which really doesn't exist.
There are an infinite number of numbers:
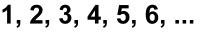
The number of odd numbers is infinite:
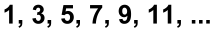
The number of even numbers is infinite:
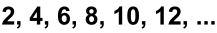
This means that the number of even numbers, or the number of odd numbers that exist, is the same as the number of all numbers!
In other words:
If you take every second number out, and only count those odd ones left, you still have the same amount of numbers!
These two sets are the same size.
It's because they're both infinite in length.
|
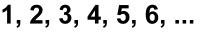
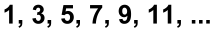
|
Isn't that en extraordinary statement? Take the set of Natural numbers, and throw half of them away. You still have as many left as when you started!
Here's the proof. You can match each Natural number with an odd number, one-on-one. Go as far as you want; there's always a matching pair. This means that the number of elements in each set must be the same.
|

|
We can show in a similar fashion that the number of numbers in the set of Natural numbers:
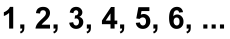
is the same as the number of numbers in the set of Whole numbers:
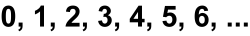
even though this second set clearly seems to have one more number in it. It does, but the size of both sets is still infinite. Both sets have the same number of elements!
This implies that 'infinity + 1' equals 'infinity'. In fact, you can add as many numbers to an infinitely long set (or take as many out as you want) and the new set you get is still infinite in length. Infinity plus or minus anything still equals infinity.
Moreover, if we take the set of Integers: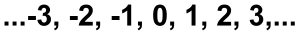 which continues on to infinity in both directions, it has the same number of numbers in it as all the previous sets! which continues on to infinity in both directions, it has the same number of numbers in it as all the previous sets!
Here's the proof:
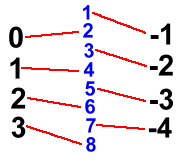
Take the set of Integers and split it into two parts; put everything from 0 and up on the left, and put all the negative numbers on the right. Then list the Natural numbers in the center.
Match the odd Natural numbers one-on-one with the Integers on the right. Match the even Natural numbers one-on-one with the numbers on the left.
Every Integer gets matched with exactly one Natural number. There must be the same number of numbers in each set!
|
|
We're not done yet! Consider the set of rational numbers: This includes all the Integers, off to infinity in both directions. But it also includes an infinite number of decimal numbers between each and every pair of Integers. An infinity of infinities, if you like.
This includes all the Integers, off to infinity in both directions. But it also includes an infinite number of decimal numbers between each and every pair of Integers. An infinity of infinities, if you like.
There are the same number of numbers here as in the simple set 0, 1, 2, 3, 4, ...
Both sets have an infinite number of elements. Clearly, 'infinity + infinity + infinity + ....' still equals infinity.
Now things start to get weird. A famous mathematician named Georg Cantor proposed and demonstrated that this infinity is actually the smallest infinity of three different infinities!
He called the infinity that we've been looking at 'aleph zero', using the symbol aleph from the Hebrew alphabet:
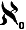 represents the number of numbers, of any kind. It's the infinity you're familiar with. represents the number of numbers, of any kind. It's the infinity you're familiar with.
But there are bigger infinities!
A point, in mathematics, is considered to be an infinitely small dot; a position without length or width.
- the number of points on a line is greater than the number of numbers.
He called this infinity 'aleph one':
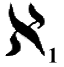
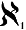 represents the number of points on a line, on a flat shape, or in an enclosed volume. represents the number of points on a line, on a flat shape, or in an enclosed volume.
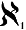 is greater than is greater than 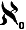
Now consider all the possible curved shapes you can draw. ALL the possible shapes:
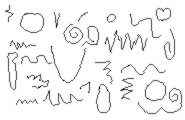 Cantor stated and proved that the number of these curves is infinite, but there are more of them than there are points on a shape, or numbers. He called this infinity 'aleph two':
Cantor stated and proved that the number of these curves is infinite, but there are more of them than there are points on a shape, or numbers. He called this infinity 'aleph two':
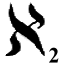
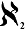 represents the number of different curves you can draw. represents the number of different curves you can draw.
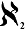 is greater than is greater than 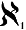 which is greater than which is greater than 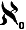
Neither Cantor nor anyone since has been able to conceive of anything which would require a fourth infinity ... it seems that three infinities may be are all there are!
Main Page
|