 In mathematics and science, an inverse-square law is any law stating that the observed "intensity" of a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. A number of physical properties get smaller as they get farther apart in a way that can be represented by an inverse square law. This means that the intensity of the property decreases in a particular way as the distance between interacting objects increases. Specifically, an inverse square law says that intensity equals the inverse of the square of the distance from the source. For example, the radiation from a point source gets smaller, the farther away it is. If the source is 2x as far away, it's intensity is only 1/4 as much. If it's 10x farther away, the intensity is 1/100. Another example is the gravitational force between two masses. As the distance between two masses increases, the force of gravity between them gets smaller as the square of the distance. For example, if the distance increases so the masses are three times farther away, the force will be one-ninth of what it was. (1/32) Let's look at what this looks like graphically. The inverse square law for electromagnetic radiation describes that 'light intensity is inversely proportional to the distance squared from the source of radiation'. 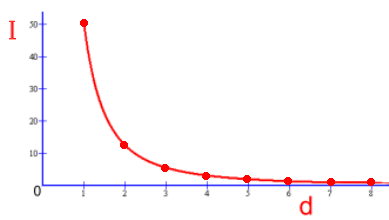
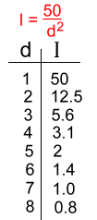
Inverse square graphs drop very quickly. Look at the intensity when d is 2 ... it's 12.5 Doubling the distance to 4 results in an intensity of 3.1, which is 1/4 as big. Notice also that as d gets larger and larger, the values of I are approaching zero, but will never get there. This is asymptotic behaviour. |