|
The Pythagorean Theorem is one of the oldest, most well-known and widely used mathematical relationships in history. It's been a fundamental part of math classes around the world for several thousand years. First described by the Greek mathematician Pythagoras 2500 years ago, the Pythagorean Theorem describes the relationship between the three sides of a right triangle. 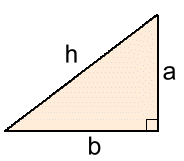 In any right triangle, the hypotenuse h is the longest side. The three sides are related in such a way that if you square the length of the hypotenuse, you will get the same answer as you do when you square each of the other two sides, and add the values together. 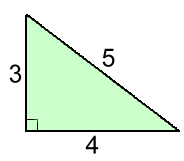 For example, consider the triangle at the right. It has a 90° angle, and sides 3,4,5 cm.
For example, consider the triangle at the right. It has a 90° angle, and sides 3,4,5 cm.The Pythagorean Theorem says that the three sides must follow this rule: 52 = 32 + 42 It works, as you can see: 25 = 9 + 16 The Pythagorean Theorem can also be expressed a different way. If you draw the triangle with squares on each side, it would look like this: 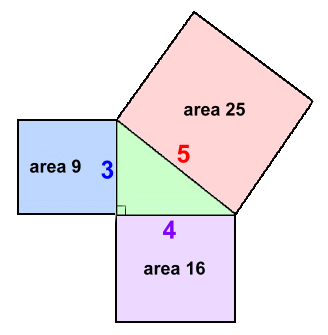
The theorem tells us that 52 = 32 + 42. This is equivalent to stating that the area of the square on the hypotenuse is equal to the areas of the squares on the other two sides, added together. Or, in other words, 25 = 9 + 16 This will only work for a right triangle. In fact, one of the first uses for this theorem thousands of years ago (when there were no accurate surveying instruments) was to help farmers lay out a 90 degree angle on the ground so they could build a proper fence between their land and their neighbour's. The method involved preparing a rope with knots tied in it: This resulted in a 90 degree angle, which the farmer could use to lay out his fence line. In modern times, the theorem is used to solve for a missing side in a triangle (more about that on page 2), and is also fundamental to the theorems in trigonometry. The sides of a right triangle can be any length, of course. We've already seen that 52 = 32 + 42. There are other whole numbers that also work: Numbers which can be sides of a right triangle (ones that follow the rule h2 = a2 + b2) are called 'Pythagorean Triples'. Here are the most common ones: In addition, any multiple of these also work: For example: 3,4,5 or 6,8,10 or 9,12,15 or 12,16,20 ... etc or these: 5,12,13 or 10,24,26 or 15,36,39 or 20,48,52 ... etc or these: 7,24,25 or 14,48,50 or 21,72,75 or 28,96,100 ... etc Let's try one: In other words, any size of right triangle will work! Now let's look at how the Pythagorean Theorem can be used to solve for a missing side in a triangle. Move on to page 2 >>> |