 value for the speed of light using a microwave oven and a chocolate bar! 
Pictured at the right are the tools you will need.In addition to a metric ruler and two toothpicks, you will need a fairly large chocolate bar with a flat bottom. The chocolate bar will still be edible after you're done, although it will have several holes melted in it. You will need a microwave oven as well, of course. Also useful would be some paper and a pencil to record your work, and a calculator. The first step is to open the microwave door and look along the edge to find the frequency of the microwaves it produces. You will see the word 'frequency', or perhaps just 'freq', with a number after it. The number you want will have units marked as MHz (megahertz). In the photo below left, you can see that the frequency of the microwaves in our oven is 2450 MHz. 
 Next, remove the wrapper from the chocolate bar and place it upside down inside the microwave near the centre. If there is a rotating dish, remove that first, and place the chocolate bar near the spindle (see photo above right).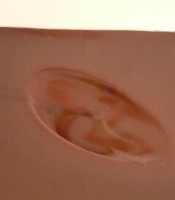 
What we going to do is to heat the chocolate bar (on 'high') just enough for it to begin to melt. Look for melted areas like in the photo at the right. It will start to melt in two places; as soon as you spot the two liquified regions, stop heating the chocolate bar and open the door. Carefully remove the bar and lay it on a smooth flat surface. Don't let the bar bend, and don't touch the melted areas. 
Now what you have to do is carefully measure the distance between the centres of the two melted regions. We did this by inserting toothpicks at the centres of these areas, as shown in the photo at the left. One of the areas was quite large, while the other was just a tiny hole.
 At the right you can see the measurement being made. We lay the toothpicks down so the ends pointed at the centres of the holes, and carefully measured the distance between the ends of the toothpicks.The value we obtained was 7.8 cm You might repeat the process with different chocolate bars and average the results. This measured distance represents half the length of a wave of microwave energy. (We'll explain why later). This means that the wavelength of the microwaves used by the device we tested is 15.6 cm Here's the calculation, using the formula for the speed of light c, a frequency f of 2450 MHz, and a wavelength λ of 15.6 cm:  You can see that we didn't get a very accurate result. But this a simple calculation yields a result that is reasonably close to the correct answer, without a lot of effort ... and we get to eat the chocolate bar too! For those who would like to see an explanation of how a microwave works and why the holes were melted in the chocolate bar exactly half a wavelength apart, go on to the second page. and The Speed of Light (an explanation of how it was originally measured) |