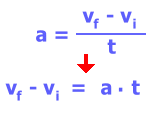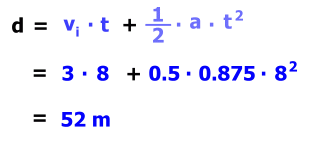On this page we'll show you how to determine displacement from a velocity graph, both when velocity is constant and when there is acceleration. Then we'll derive the displacement formula, for use when there is acceleration. To begin, let's look at constant velocity. In the first graph below you can see the result of an object moving at a constant velocity of 6 m/s for a time interval of 8 seconds. 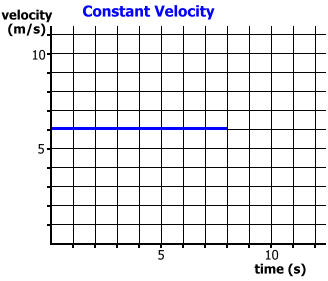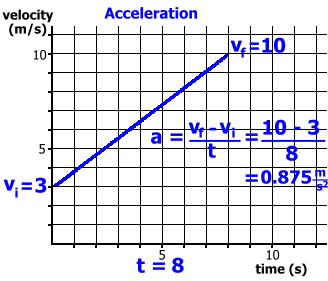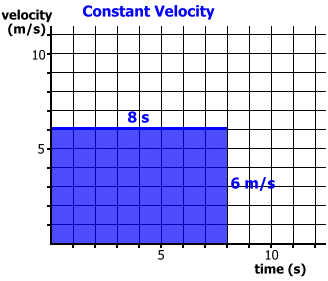In order to find the displacement after 8 seconds, we will find the area between the graph and the horizontal axis, as shaded in the diagram at the right, above. Displacement = area of rectangle = 6 m/s x 8 s = 48 m Since there is no acceleration, this is equivalent to using the formula d = v · t Here's an example where there is acceleration. We'll begin with the case where an object starts from rest. 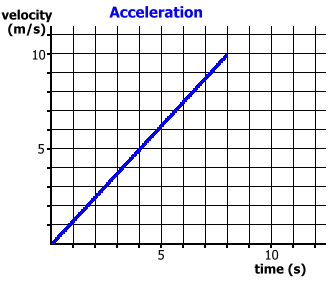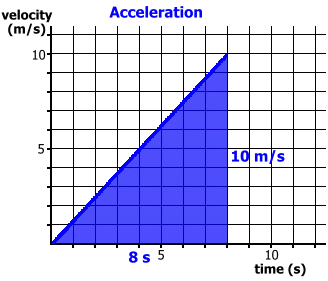In order to find the displacement after 8 seconds, we will find the area between the graph and the horizontal axis, as shaded in the diagram at the right, above. Displacement = area of triangle = (8 s x 10 m/s)/2 = 40 m Since there is acceleration, and  vi = 0, this is equivalent to using the formula d = 1/2 · t · (vf - vi) Finally, let's examine the case where there is acceleration, but the initiial velocity is not zero. 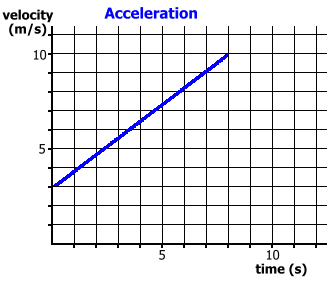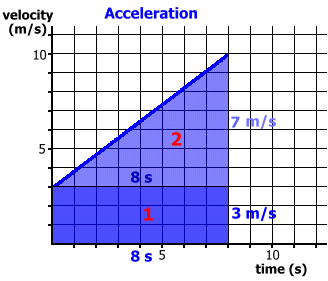Again, we need to find the area under the graph, but it's a little more complicated this time because the area is not a simple shape. In order to find the area under the graph, we've divided it into two regions, numbered 1 and 2. Region 1 is a rectangle, and region 2 is a triangle. We'll work out the area of each region and add them together: In other words, for an object whose velocity increases from 3 m/s to 10 m/s in a time of 8 s, the displacement will be 52 m. This is equivalent to using the formula:   d = vi · t  +  1/2 · a · t2   We'll show you where this formula comes from: In order to derive the displacement formula, we'll need to make a substitution. We will replace the expression  (vf - vi) by the simpler expression  a · t You can see why they're equivalent by looking at the rearrangement at the right. We're going to redo the calculation we did earlier, but this time we won't specify actual numbers. Instead, we'll use vi, vf and t. We'll calculate areas 1 and 2 again, using the area formulas for a rectangle and triangle. 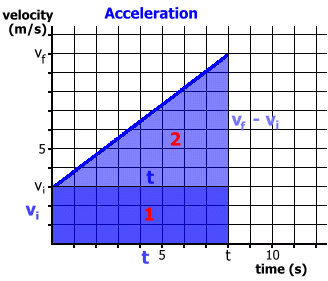Notice in line 4, above right, we replaced (vf - vi)  for  a · t, as we said we would. The final step gives us the standard formula for displacement:   d = vi · t  +  1/2 · a · t2 Now we'll redo the example from above, using this formula: Try a Quiz Resources