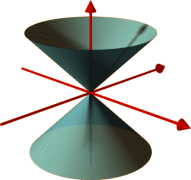
  
A true cone has two 'naps', each of which extends to infinity upwards and downwards. The two naps meet at a point in the centre.
For purposes of measurement geometry, we will use just one nap, and call that a cone. It can be used in any orientation; here (at right) we have the point up.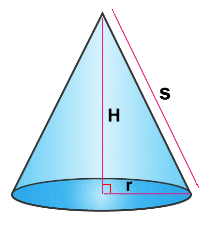 
Characteristics of a ConeThe base is a circle, with radius r The height down the centre is the height H The length down the side is the slant height s Because of the right angle, you can find any missing one of these three measurements by using the Pythagorean Theorem. We will look at how to calculate the volume and surface area of a cone. We'll also look at problems where you know the answer and must find one of the cone's measurements by solving backwards. We'll also try some questions where a missing measurement must be determined first. Finally, we'll try some mixed problems. In all of our examples, we will assume that you are proficient at solving simple equations. |